The Kaleidoscope competition is returning to Logic Masters India this weekend! It will feature 14 new puzzles from the past 7 Kaleidoscope types, and will take place from 10/19 to 10/22, starting in a couple hours. See the instruction booklet and discussion forum by clicking the image or link below.
Category: Puzzle
Omni-Yajilin
My first Nikoli puzzle book was Pencil Puzzle Yajilin 1, back in 2006 when the Pencil Puzzle series was available. Yajilin has always been a special puzzle type for me. It marks the beginning of that unscratchable itch that I think most puzzlers have, to relentlessly explore new puzzle types and variations and to engage with problems for which no well-trodden inventory of techniques already exists. I’m happy to return from my break with a Yajilin variation on a new tiling [33434; 3262; 3446; 63].
EDIT: Following a suggestion from edderiofer, I have made the clue cells easier to distinguish.
EDIT 2: Puzzle number 3 has been corrected. The far right hexagonal clue should have been a 3.
Rules
Shade some cells and draw a loop in remaining cells such that:
- Every empty cell is either shaded or part of a single loop that does not branch or intersect.
- Numbers in some cells indicate the total number of shaded cells that can be seen in all directions from that cell. Lines of sight run perpendicular to the edges of a cell and terminate on the edge of the grid or at a triangular cell, counting that cell.
Example


Puzzles
All of the puzzles can be found organized in this printable PDF, or in the images below.
PDF Omni-Yajilin
01. Medium
02. Hard
03. Medium

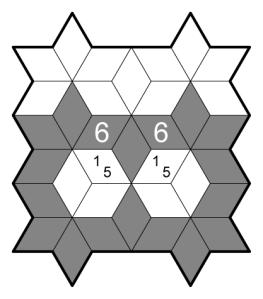
Hexagonal Kurokuron
Kurokuron (クロクロ一ン: “black clone”), is a shading puzzle that first appeared in Puzzle Communication Nikoli issues 153-155. Identical rules apply to a hexagonal grid.
Rules
Shade some cells such that:
- Bold-outlined regions contain exactly two shapes, made up of contiguous groups of 1 or more shaded cells. Within a region, the two shapes must be congruent, allowing reflection and rotation.
- A shape cannot share an edge with another shape.
- Cells with arrows, which cannot be shaded, point to a neighboring cell, which must be shaded and part of a shape consisting of the given number of cells.
Example


Puzzles
All of the puzzles can be found organized in this printable PDF, or in the images below.
01. Easy
02. Medium

03. Medium

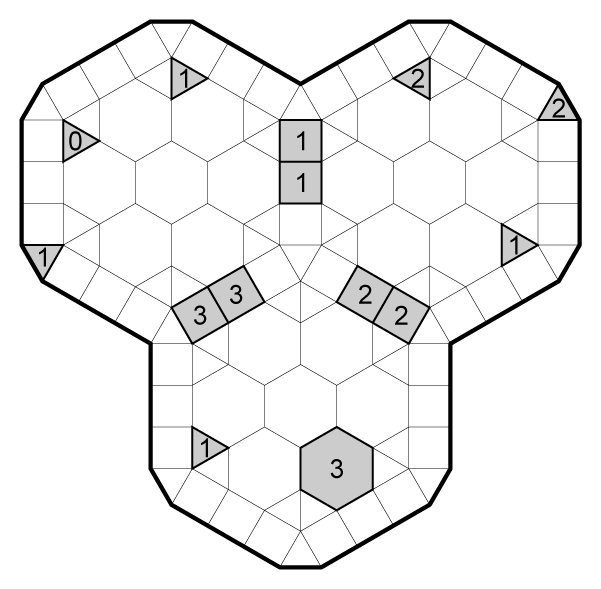
Karst
Rules
Variant of Cave:
- Draw a single loop along the dashed lines that encloses some cells. Edges of this loop may not cross or share a vertex.
- Numbers indicate the number of connected cells from all lines of sight radiating from that cell, including the cell itself. Numbers can be inside or outside of the loop. Lines of sight end on either the edge of the grid, the center of a triangular cell, or the edge of the loop.
Example

Puzzles
All of the puzzles can be found organized in this printable PDF, or in the images below.
PDF Karst
01. Medium
02. Hard

03. Hard

Sudoku embedded in a Kakuro
Rules
In addition to standard Kakuro rules, the grey shaded cells must form a valid Sudoku solution
The puzzle below has been corrected. See here for a highlight of the correction.
Puzzle
The puzzle can be found in this printable PDF, or in the image below.

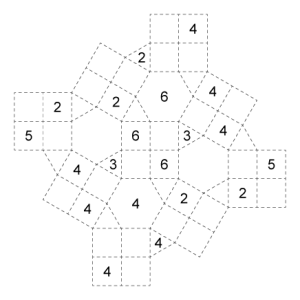
Sum Star
Here’s a type that came together in my notebooks back in October 2016. It’s nearest rectangular precedent is Gapped Kakuro by Serkan Yürekli. A puzzle of this type will be featured today on Grandmaster Puzzles.
Rules
Fill cells with numbers and shade all remaining cells such that:
- Each dodecagon contains the numbers 1-9 exactly once.
- Numbers in cells sharing a vertex with a black triangle add up to the indicated sum without repeating.
- A shaded cell cannot share an edge with another shaded cell.
Example


Puzzles
All of the puzzles can be found organized in this printable PDF, or in the images below.
PDF Sum Star
01. Medium
02. Hard

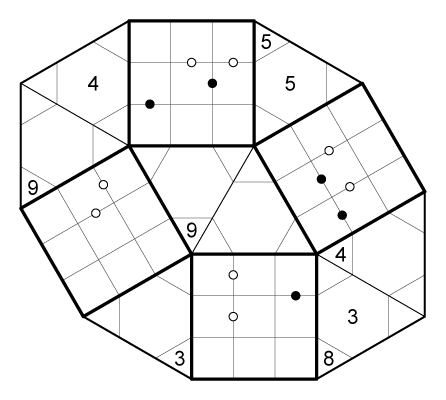
Kropki Switch
This may be the most obscure puzzle idea I’ve come up with yet. Even though it’s hard to explain, I like how it solves.
Rules
Place the numbers 1-9 so that they appear exactly once in each 3×3 block of square cells.
Standard Kropki rules apply to borders between square cells:
- A black dot on the border between two square cells indicates that the ratio of those cells is exactly 2. A white dot on the border between two square cells indicates that the difference between those cells is exactly 1. A border between two square cells with no dot indicates that neither of these properties applies. (The border between “1” and “2” could have either a black or a white dot.)
Between the 3×3 blocks of square cells are switches, which consist of 3 triangles and 1 hexagon.

Exactly one cell from each switch must be shaded (for double switches, one cell from each side must be shaded). Shaded cells cannot share an edge. A switch relates triplets from different 3×3 blocks in the following three possible combinations: one triangle, one hexagon, or two triangles.

If the switch cell (or one of the two cells in the case of two triangles) is shaded, both triplets must contain the same three numbers. If the cell (or both cells in the case of two triangles) is unshaded, both triplets must contain different numbers. If a switch cell containing a number is shaded, any triplets touching that cell must contain that number. If the cell is unshaded, any triplets touching that cell must not contain that number.
Example


Puzzles
All of the puzzles can be found organized in this printable PDF, or in the images below.
PDF Kropki Switch
01. Medium
02. Hard
03. Expert

Rhombile Transparent Tapa Loop
Here is a transparent variation of Tapa-Loop by Serkan Yürekli adapted to a Rhombile grid. Some puzzles of this type crafted by Serkan and Fatih Kamer Anda will be featured on the upcoming Tapa Variations Contest hosted by Logic Masters India.
Rules
Shade some cells such that:
- For any cell with one or more numerical clues, shaded cells form connected groups of the indicated size within the group of cells sharing a vertex with the clued cell. Cells with clues can be shaded.
- For every vertex touching exactly 3 cells, at least one cell must be unshaded.
- One must be able to draw a single loop through all shaded cells.
Example

Puzzles
All of the puzzles can be found organized in this printable PDF, or in the images below.
PDF Rhombile Transparent Tapa Loop
01. Medium
02. Hard

03. Easy

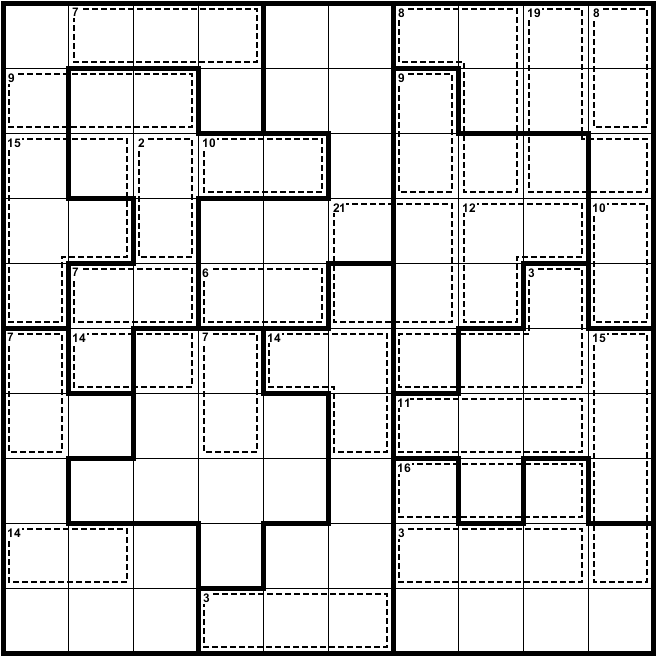
Killer Sudoku Hybrids
Over these last few weeks I’ve returned to my roots with a few Killer Sudoku variants, which I recently posted to the Daily League on Facebook. I have a few more ideas, but they’ll have to wait until after finals.
Star Battle Killer
Place the numbers 1-8 and two stars in each row, column, and jigsaw group. Stars cannot touch each other, even diagonally. Numbers cannot repeat within cages. Stars count as 0 in cages.
Butterfly X Nurikabe Killer
This puzzle is made up of four overlapping 9×9 Sudoku grids arranged in a butterfly pattern (1 in each corner), each with it’s own set of main diagonals, which must contain the numbers 1-9. The sum/size of all cages are given, but not their shapes. The shapes of cages must form islands in a valid Nurikabe solution. Givens are shaded, and thus cannot be part of a cage.

Killer Battleships
Classic Sudoku rules apply. Additionally, a fleet of battleships must be placed into the grid, such that they do not touch, even diagonally. Cells occupied by the battleships must add up to the sum associated with each ship, and any cell sharing an edge with a ship cannot contain any of the numbers inside the ship. Numbers on the outside of the grid indicate how many cells in that row or column are occupied by a ship. Givens are “sea” squares, and cannot contain a ship.

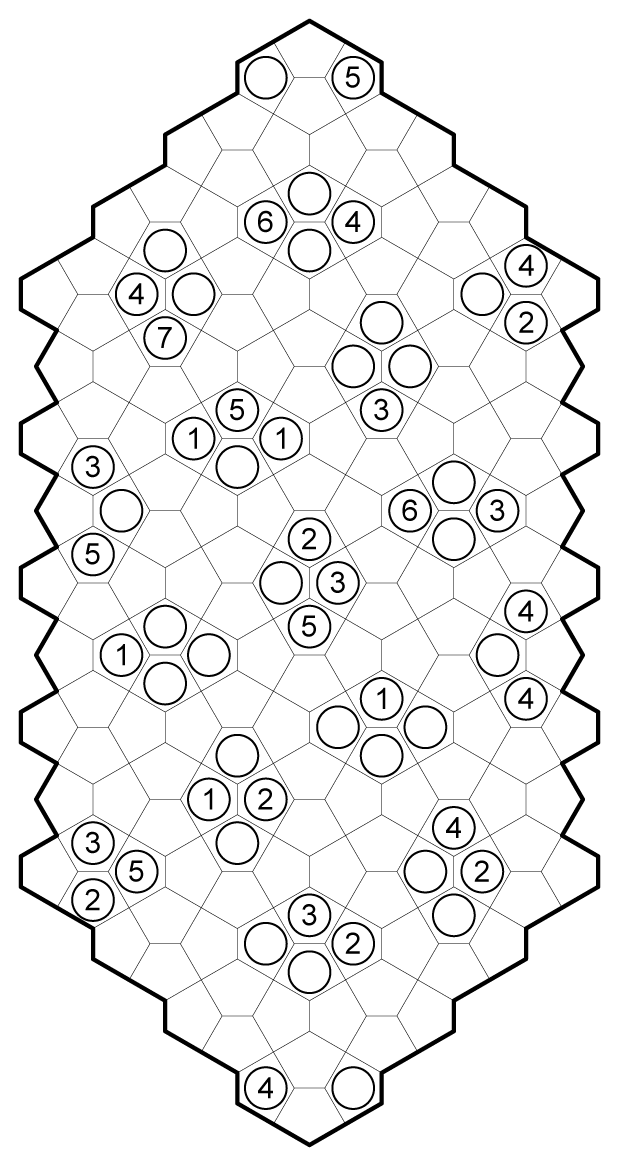
Cairo Pentagonal Kurotto
Here is an adaptation of Nikoli’s Kurotto to a Cairo Pentagonal grid.
Rules
Standard Kurotto Rules. Shade some cells such that:
- Each circled number equals the total number of cells in all edge-connected clusters touching that cell.
- Cells with circles cannot be shaded.
Example


Puzzles
All of the puzzles can be found organized in this printable PDF, or in the images below.
01. Medium
02. Hard

03. Hard